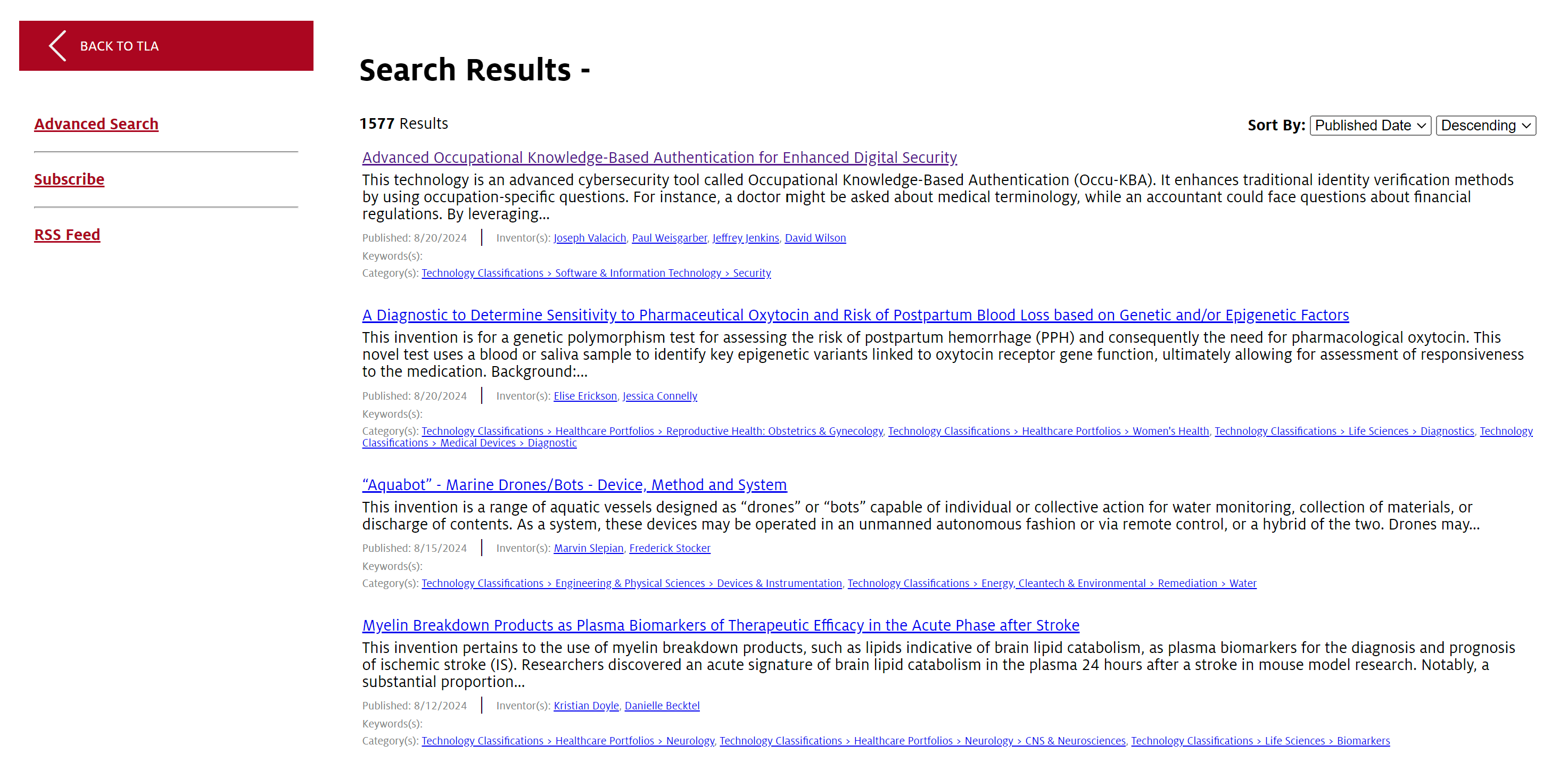
Data Analysis and Model Creation
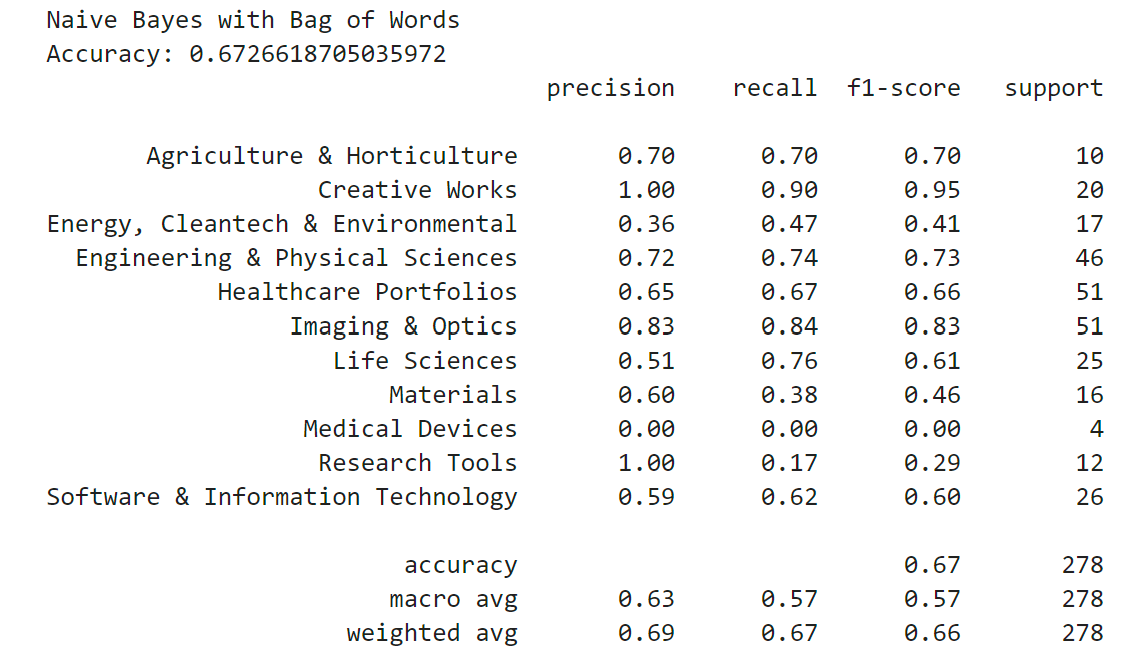
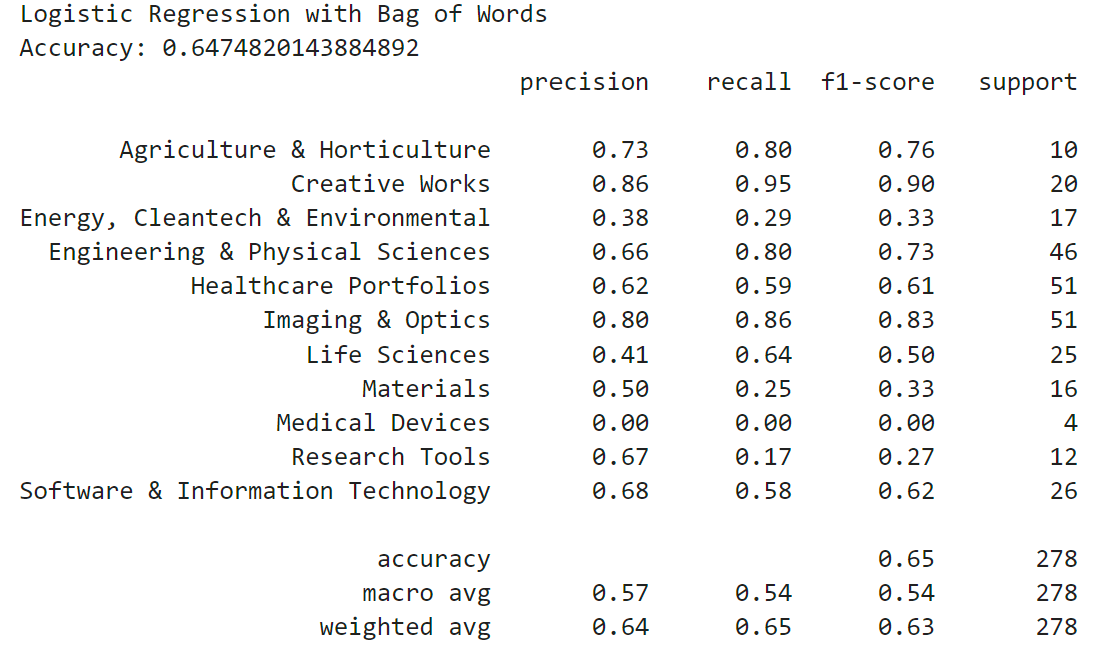
Now that I had my dataset, it was time to start building the different models to test. To build and train these models, I had to convert the text data into a numerical representation that the model can work with. There are several ways to create word vectors, but two common ones are the Bag-Of-Words model and the term frequency-inverse document frequency (tf-idf) model. I first split the data into training and test sets so that each model could be trained on the data and tested on its accuracy. The first word embedding I used was the Bag of Words model. This model represents text as an unordered collection of words. This model does not take into account word order, it just uses the frequency of the word as a feature. To do this, I used the CountVectorizer tool from scikit-learn. This transforms a given text into a vector based on the frequency of each word. I also chose the parameters to remove stop words from the data, which are commonly used words that do not provide significant meaning to the data.
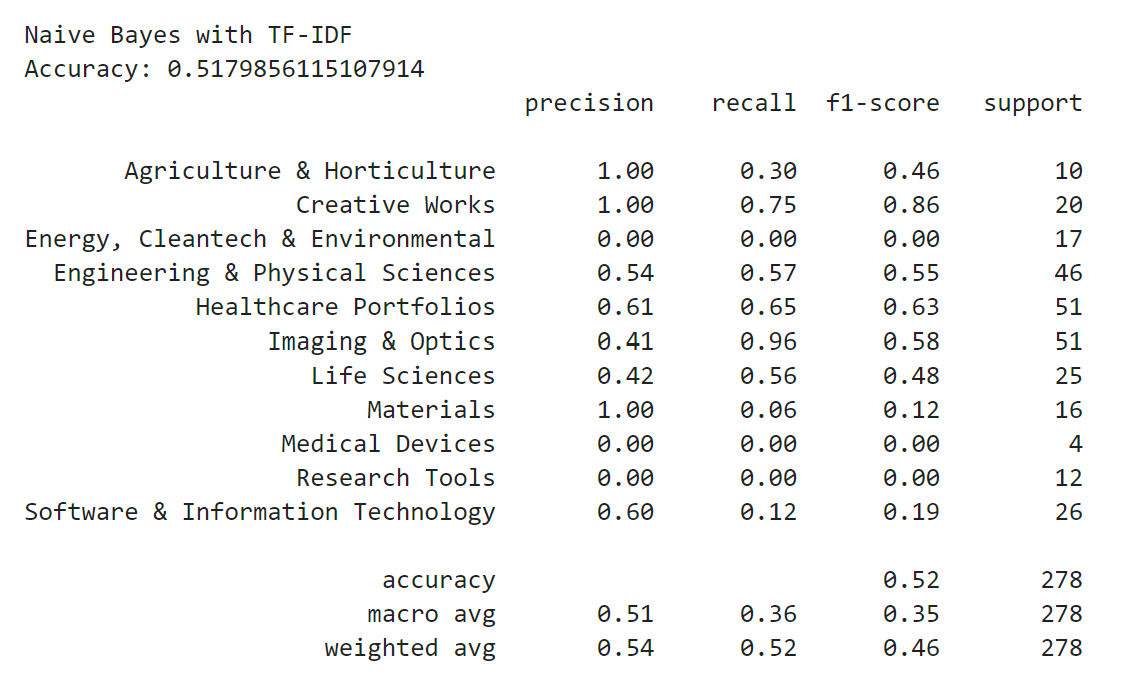
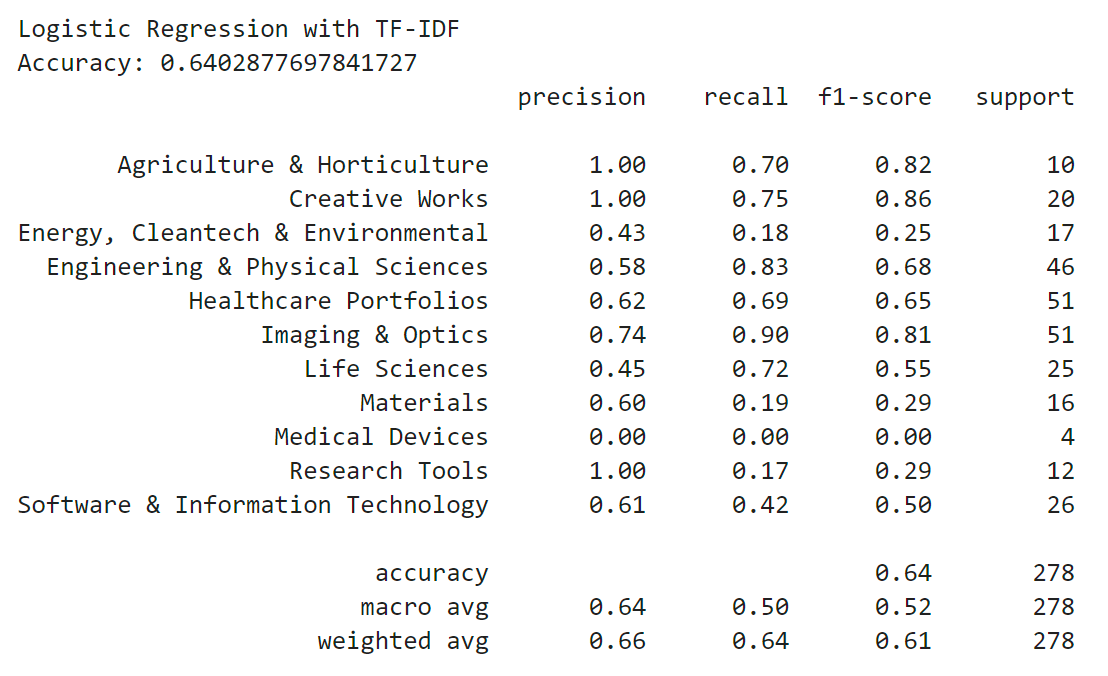
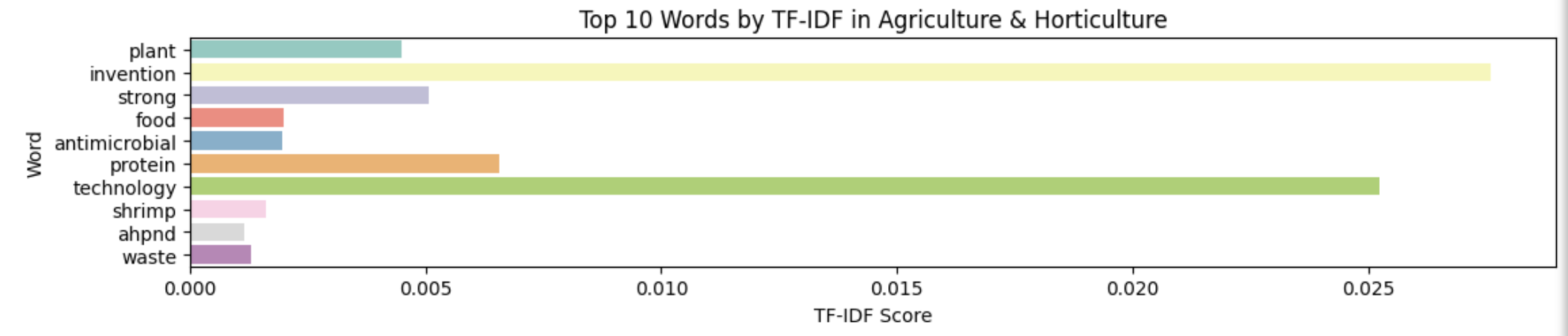
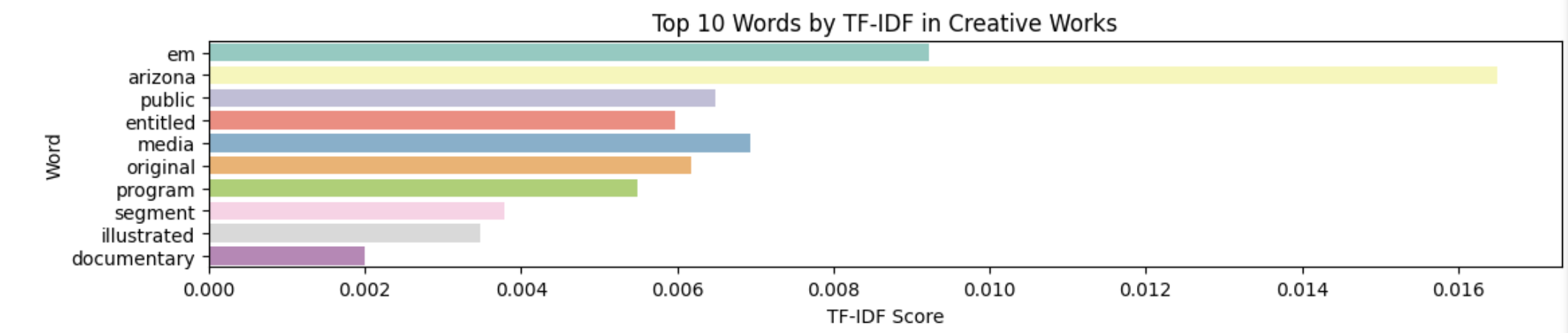
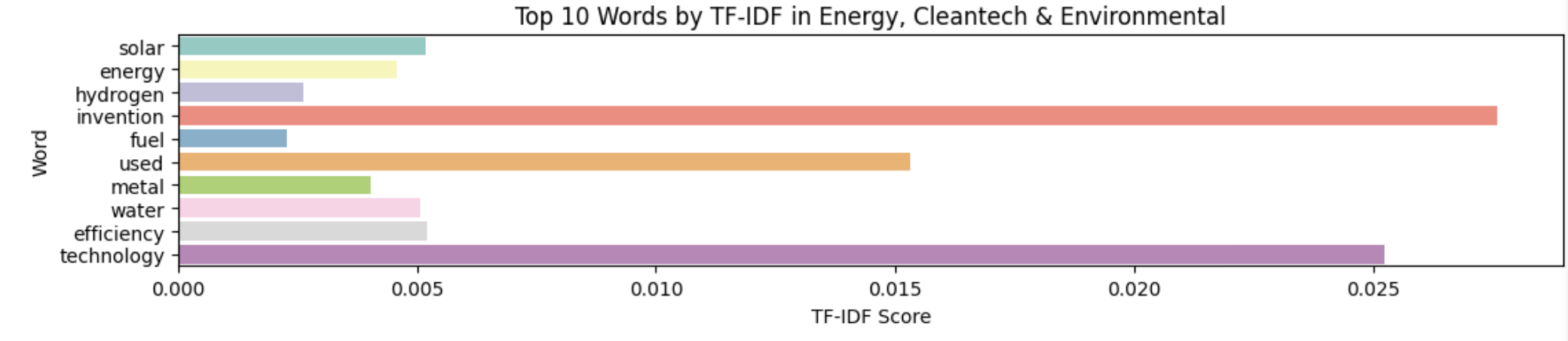
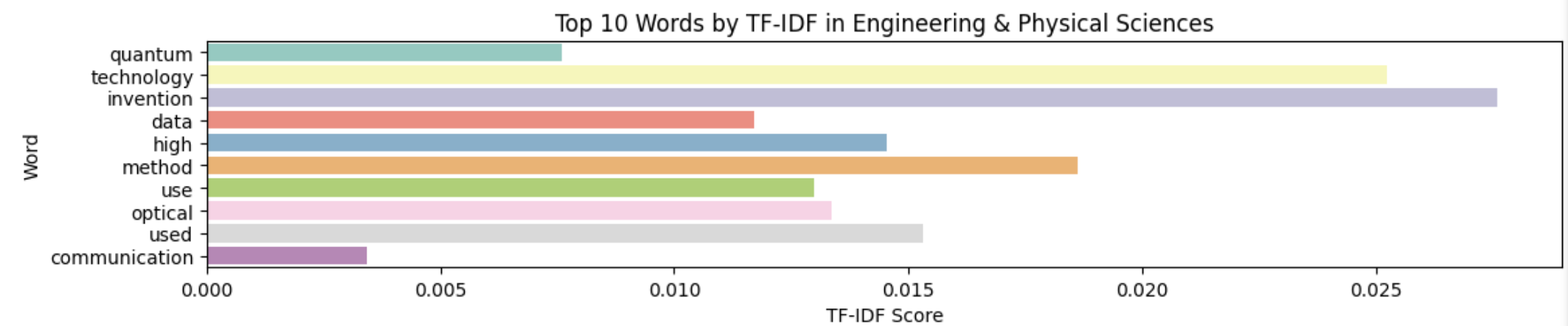
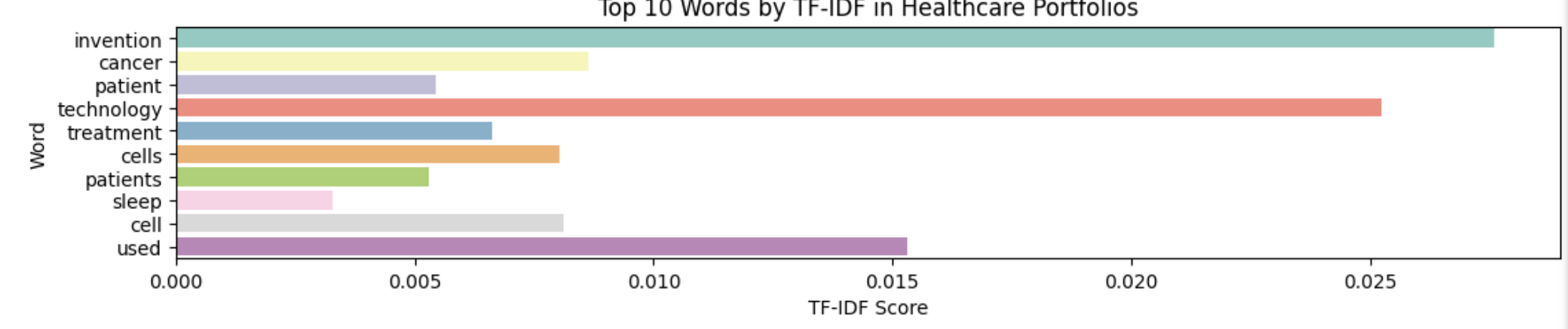
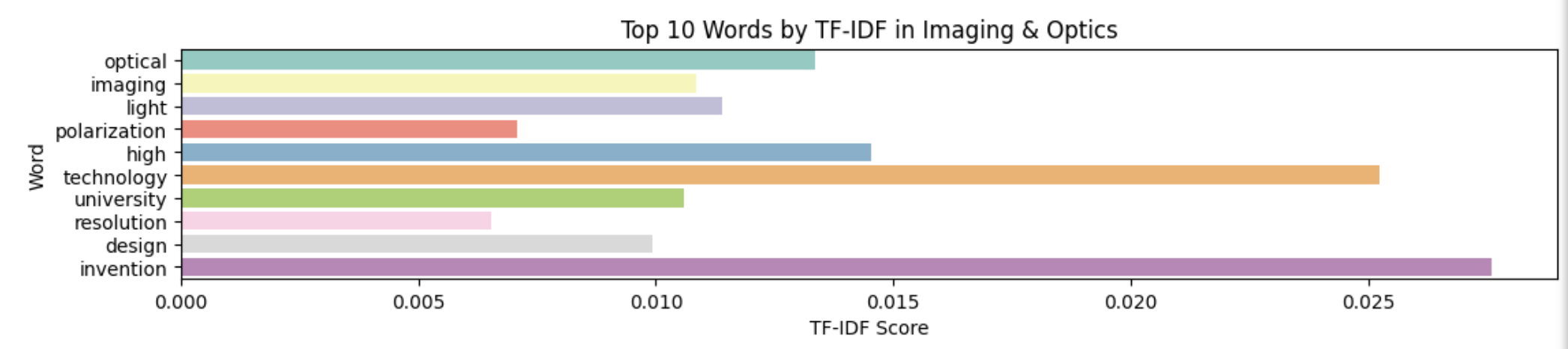
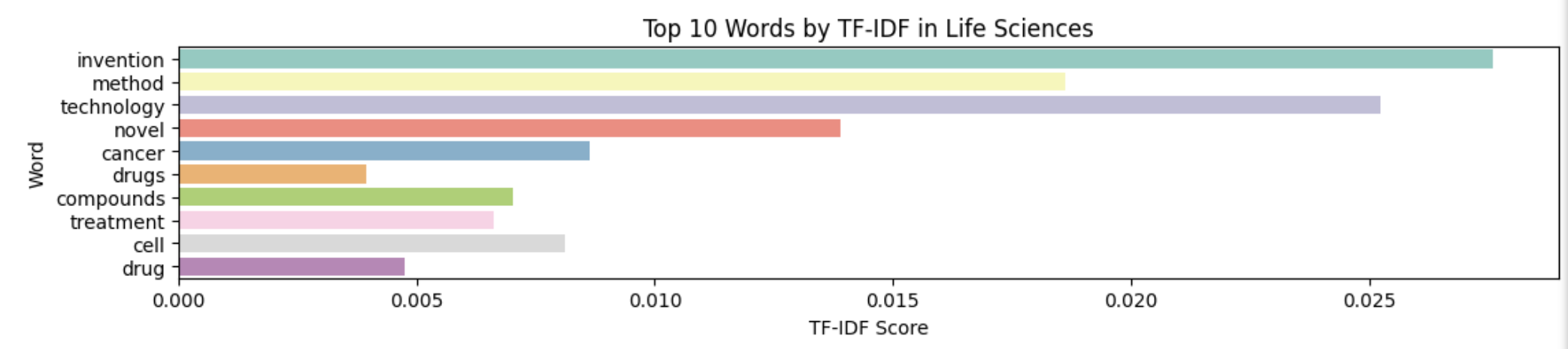
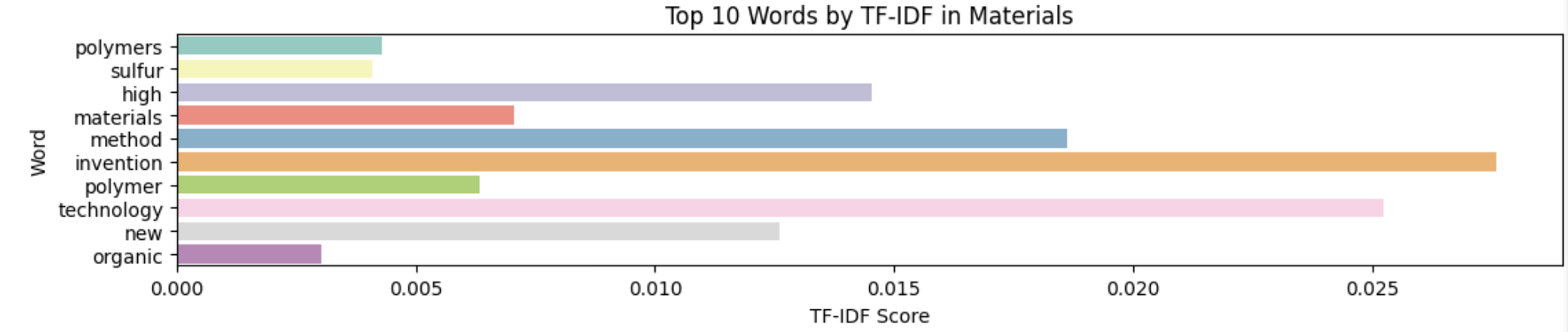
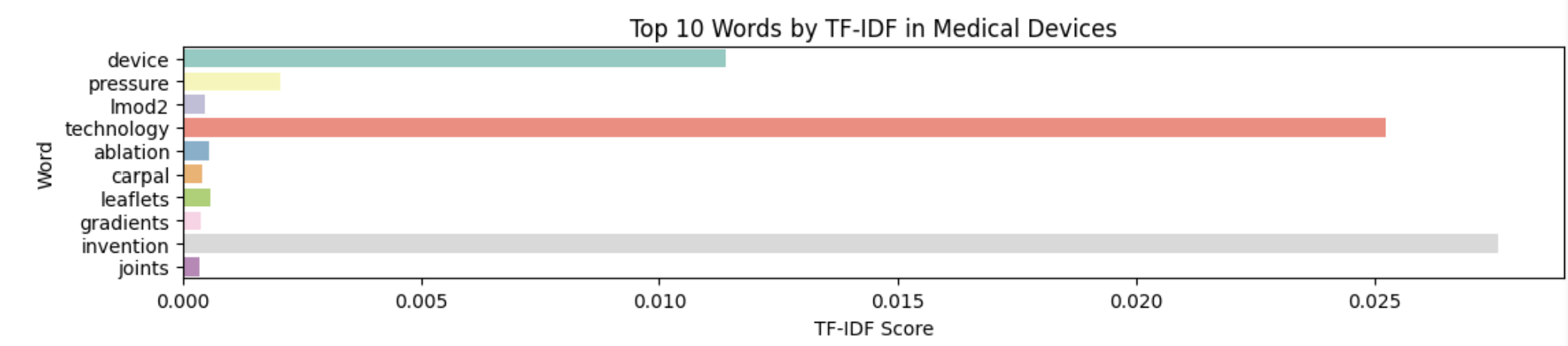
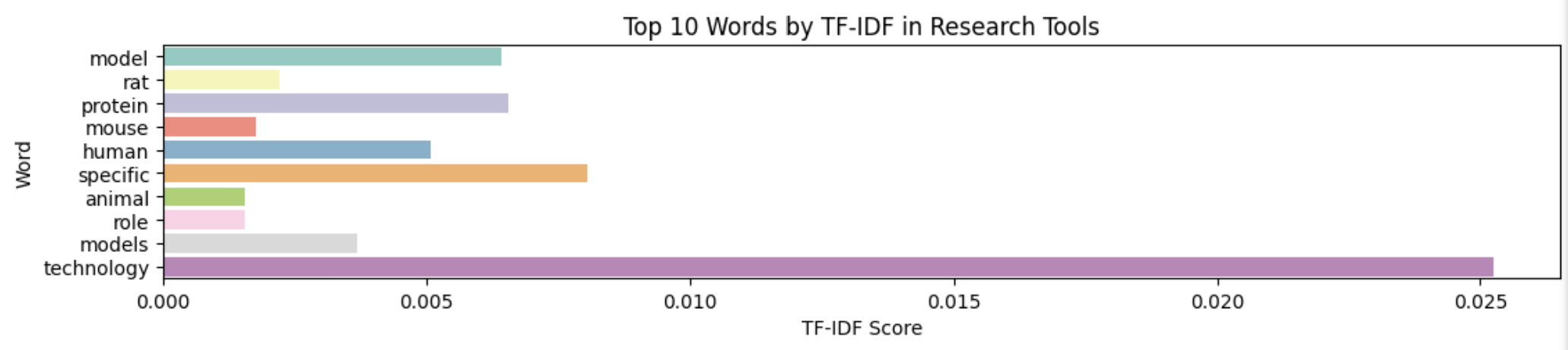
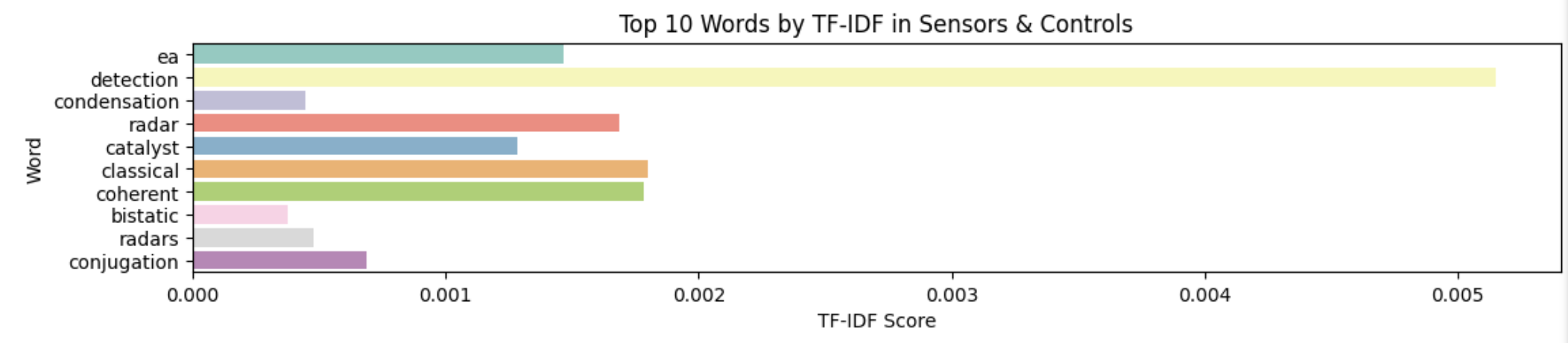
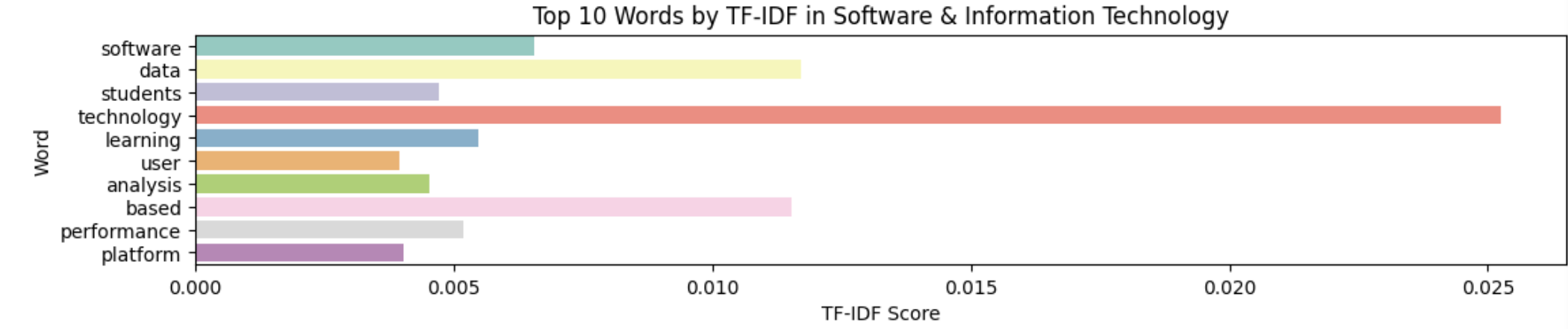
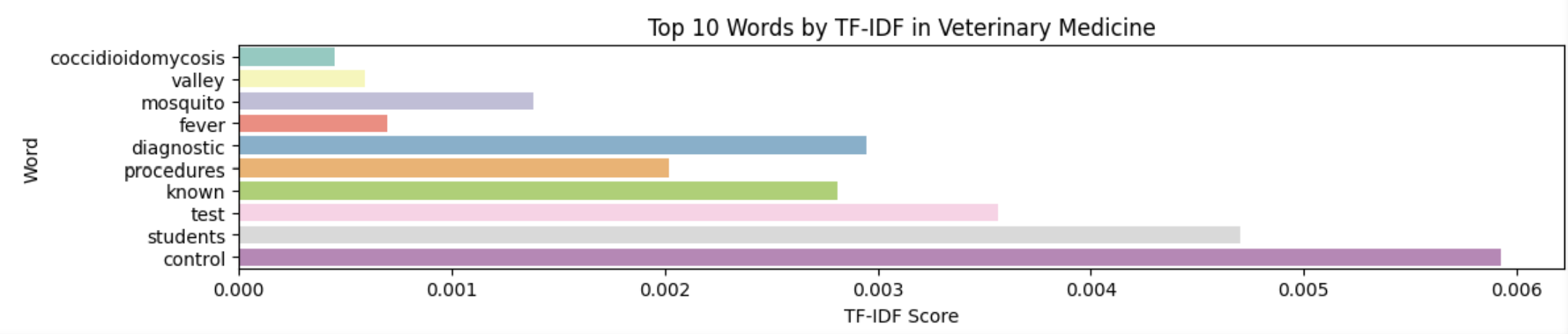
The next word-embedding model I used was the tf-idf model. This model is better at ignoring common words and places more importance to rarer words. Unlike Bag of Words, it assigns weights to words based on their importance in the document and corpus. I used the TfIdfVectorizer tool from scikit-learn to create this model, again filtering out stop words.
Now that I had two different numerical representations of the text data, I could compare different classifier models. The first model I wanted to test was Naive Bayes. Naive Bayes is a probabilistic classifier that assumes independence and uses conditional probabilities to find the probability of a class for a given data point. I fit the bag-of-words feature data on one multinomial Naive Bayes model and I fit the tf-idf feature data on another multinomial Naive Bayes model.
I wanted to compare the Naive Bayes model with a logistic regression model. Naive Bayes is a generative model and estimates the probability of each class based on Bayes' Law to predict the label for a data point, whereas logistic regression is a discriminative model that uses the logistic function to map data points to labels. Logistic regression tends to perform better at more complex text classification tasks. Like before, I fit the bag-of-words feature data on one logistic regression model and I fit the tf-idf feature data on another logistic regression model.
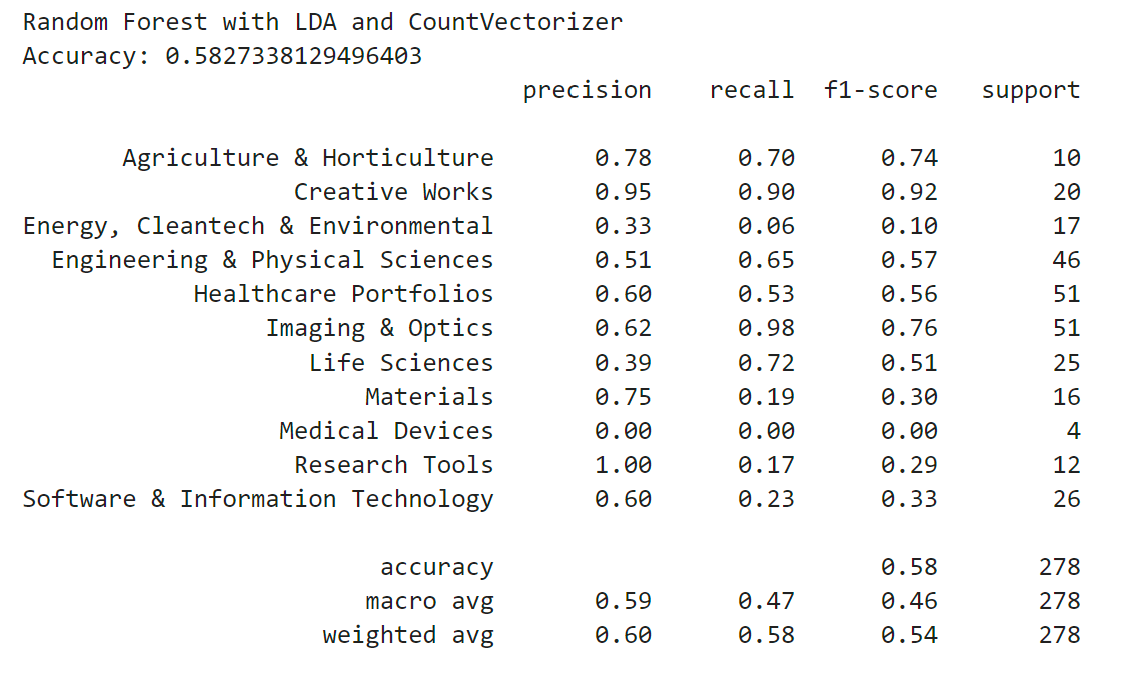
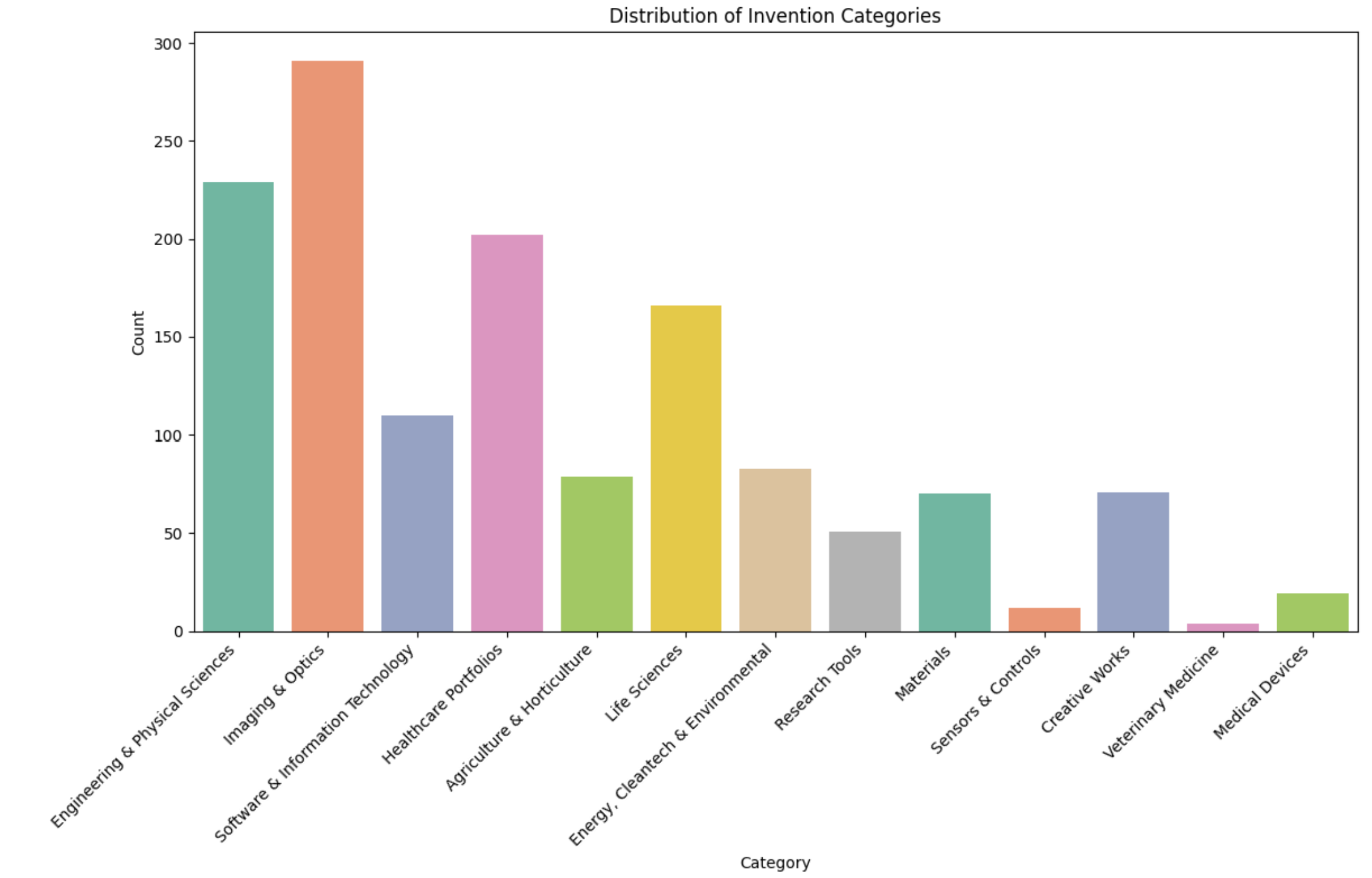
Next I wanted to test a more advanced algorithm, Latent Dirichlet Allocation (LDA). LDA is a generative model based on the bag-of-words model. LDA is a topic modeling algorithm that is used for discovering topics in a piece of text. I used the module from scikit-learn and applied the bag-of-words data to the model with a value of 13 topics (the number of potential categories the invention could be classified as).
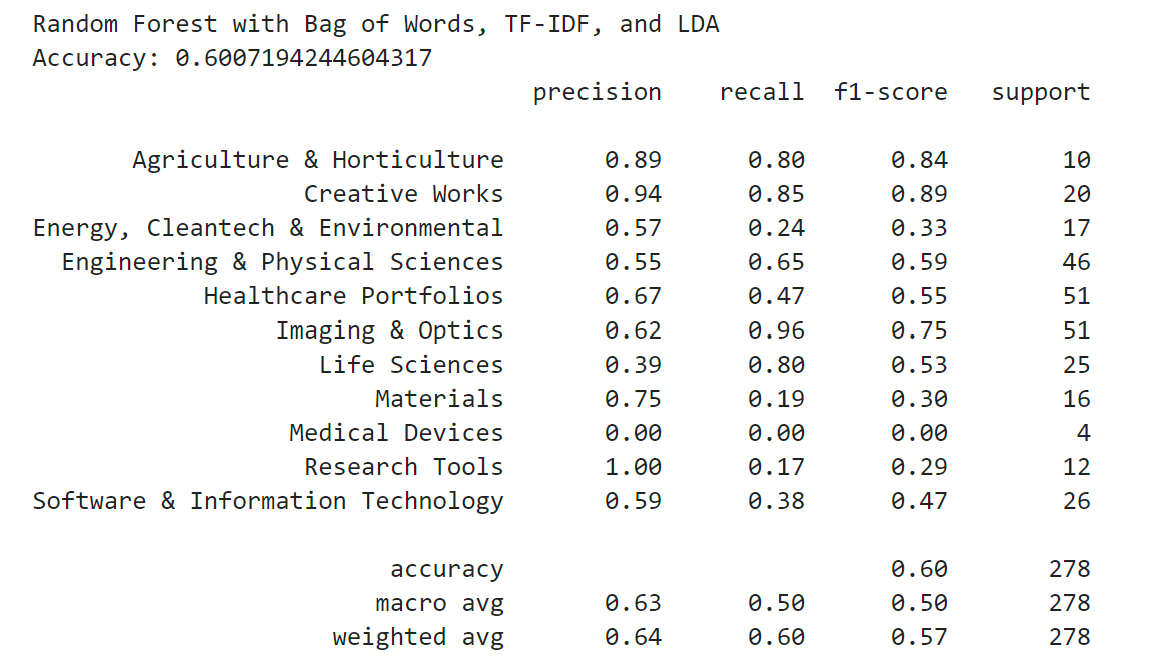
Finally, I wanted to combine the bag-of-words features, the tf-idf features, and the LDA model to see if this would result in the best accuracy. I vectorized the data using CountVectorizer for bag-of-words and TfidfVectorizer for tf-idf. I then created the LDA model as before, but then combined the feature vectors column-wise to create a final combined feature vector for each data point.